Algorithms-B.Tech/lectures/2.org

• Comparing Growth rate of funtions
  • Applying limit
  • Using logarithm
  • Common funtions
• Properties of Asymptotic Notations
  • Big-Oh
  • Properties

Comparing Growth rate of funtions

Applying limit

To compare two funtions $f(n)$ and $g(n)$. We can use limit \[ \lim_{n\to\infty} \frac{f(n)}{g(n)} \]

• If result is 0 then growth of $g(n)$ > growth of $f(n)$
• If result is $\infty$ then growth of $g(n)$ < growth of $f(n)$
• If result is any finite number (constant), then growth of $g(n)$ = growth of $f(n)$

Note : L'Hôpital's rule can be used in this limit.

Using logarithm

Using logarithm can be useful to compare exponential functions. When comaparing functions $f(n)$ and $g(n)$,

• If growth of $\log(f(n))$ is greater than growth of $\log(g(n))$, then growth of $f(n)$ is greater than growth of $g(n)$
• If growth of $\log(f(n))$ is less than growth of $\log(g(n))$, then growth of $f(n)$ is less than growth of $g(n)$
• When using log for comparing growth, comaparing constants after applying log is also required. For example, if functions are $2^n$ and $3^n$, then their logs are $n.log(2)$ and $n.log(3)$. Since $log(2) < log(3)$, the growth rate of $3^n$ will be higher.
• On equal growth after applying log, we can't decide which function grows faster.

Common funtions

Commonly, growth rate in increasing order is \[ c < c.log(log(n)) < c.log(n) < c.n < n.log(n) < c.n^2 < c.n^3 < c.n^4 ... \] \[ n^c < c^n < n! < n^n \] Where $c$ is any constant.

Properties of Asymptotic Notations

Big-Oh

• Product : \[ Given\ f_1 = O(g_1)\ \ and\ f_2 = O(g_2) \implies f_1 f_2 = O(g_1 g_2) \] \[ Also\ f.O(g) = O(f g) \]
• Sum : For a sum of two functions, the big-oh can be represented with only with funcion having higer growth rate. \[ O(f_1 + f_2 + ... + f_i) = O(max\ growth\ rate(f_1, f_2, .... , f_i )) \]
• Constants : For a constant $c$ \[ O(c.g(n)) = O(g(n)) \], this is because the constants don't effect the growth rate.

Properties

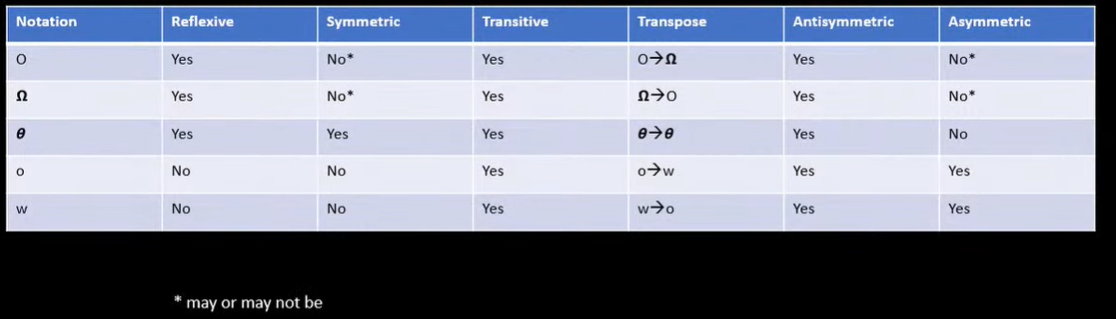
• Reflexive : $f(n) = O(f(n)$ and $f(n) = \Omega (f(n))$ and $f(n) = \theta (f(n))$
• Symmetric : If $f(n) = \theta (g(n))$ then $g(n) = \theta (f(n))$
• Transitive : If $f(n) = O(g(n))$ and $g(n) = O(h(n))$ then $f(n) = O(h(n))$
• Transpose : If $f(n) = O(g(n))$ then we can also conclude that $g(n) = \Omega (f(n))$ so we say Big-Oh is transpose of Big-Omega and vice-versa.
• Antisymmetric : If $f(n) = O(g(n))$ and $g(n) = O(f(n))$ then we conclude that $f(n) = g(n)$
• Asymmetric : If $f(n) = \omega (g(n))$ then we can conclude that $g(n) \ne \omega (f(n))$